Sevgili öğrenciler özel sayı örüntüleri konu anlatımı sayfamıza hoş geldiniz. Konu anlatımımız aşağıda yer almaktadır. Hepinize başarılar dileriz.
Özel Sayı Örüntüleri Konu Anlatımı
Özel sayı örüntülerinin bazıları aşağıda anlatılmaktadır.
Fibonacci Sayı Dizisi
» Leonardo Fibonacci 13. yüzyılda yaşamış bir İtalyan matematikçidir. Fibonacci en ünlü eseri olan Liber Abaci adlı kitabında Fibonacci Dizisini tanıtmıştır. Bu dizi 1, 1, 2, 3, 5, 8, 13, 21, 34… şeklinde devam etmektedir. Diziyi bu kadar ünlü yapan şey ise dizinin terimlerinin doğada bitkilerde karşımıza çıkmasıdır. Defne yaprağında, ayçiçeğinde, çam kozalağında bu sayılara rastlanmaktadır.
Ayrıca bu sayılar Pascal Üçgeninde, Mimar Sinan’ın eserlerinde, Leonarda Da Vinci’nin resimlerinde karşımıza çıkmaktadır.
» Dizide iki terim toplanarak sonraki terim elde edilmekte ve dizi bu şekilde sonsuza kadar devam etmektedir.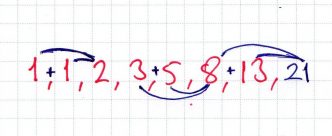
» Yukarıdaki resimde Fibonacci Dizisinin terimlerinin nasıl elde edildiği gösterilmiştir.
Üçgensel Sayılar Dizisi
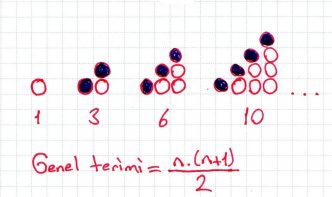» Bu sayı dizisinin terimleri, terim numarası ile terim numarasından önceki doğal sayıların toplamından oluşuyor.
» 1, 3, 6, 10, 15,… şeklinde devam eden sayı örüntüsü Üçgensel Sayılar Dizisi olarak bilinir.
» Bu dizinin genel terimi yandaki resimde
verilmiştir.
Karesel Sayılar Dizisi
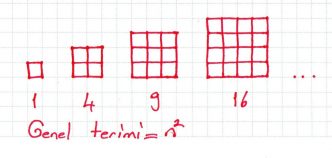» Bu sayı dizisinin terimleri, terim numarasının karesinden oluşur.
» Örneğin dizinin 15.adımında 15² = 225 tane kare vardır.
» 1, 4, 9, 16, 25,… şeklinde devam eden sayı örüntüsü Karesel Sayılar Dizisi olarak bilinir.
» Bu dizinin genel terimi yandaki resimde verilmiştir.
Aritmetik Dizi
» Bir sayıya belirlenen başka bir sayının art arda eklenmesi veya çıkarılması ile elde edilen sayıların oluşturduğu sayı örüntüsüne Aritmetik Dizi denir.
» Aritmetik Dizide ardışık iki terimin farkına (art arda eklenen veya çıkarılan sayıya) dizinin ortak farkı denir.
» Örneğin 5 sayısına sürekli 3 ekleyerek bir Aritmetik dizi oluşturalım. Bu dizinin terimleri 5, 8, 11, 14, 17, 20, 23,… şeklinde devam edecektir. Bu örnekte ilk terim 5, ortak fark ise 3’tür.
» Aritmetik dizinin genel terimi= İlk terim+ (n-1). Ortak Fark tır. Burada n adım (terim) sayısıdır.
Geometrik Dizi
» Bir sayı ile belirlenen başka bir sayının art arda çarpılması veya bölünmesi ile elde edilen sayıların oluşturduğu sayı örüntüsüne Geometrik Dizi denir.
» Geometrik dizilerde ardışık iki terimin oranına (art arda çarpılan veya bölünen sayıya) dizinin ortak çarpanı denir.
» Örneğin 64 sayısını sürekli 2 ye bölerek bir Geometrik dizi oluşturalım. Bu dizinin terimleri 64, 32, 16, 8, 4, 2, 1,… şeklinde devam edecektir. Bu örnekte ilk terim 64, ortak çarpan ise 2’dir.
» Geometrik dizinin genel terimi= İlk terim. (Ortak Çarpan)n-1 dir. Burada n adım (terim) sayısıdır.
