6.Sınıf birim küplerden hacim ölçme konu anlatımı. Hacim ölçmeyi ilk defa bu sene 6.sınıfta öğreniyoruz. Dikdörtgenler prizması, kare prizma ve küpü 5.sınıfta iken tanımıştık, temel elemanlarını öğrenmiştik ve yüzeylerinin alanını hesaplamıştık. Bu sene 6.sınıfta dikdörtgenler prizması, kare prizma ve küpün hacmini hesaplayacağız. Başarılar dileriz.
Doğru, doğru parçası ve ışın bir boyutludur, bir boyuta sahiptir. Bunlarda sadece boyut olarak uzunluk vardır. Kare, dikdörtgen, üçgen gibi şekiller iki boyutludur, iki tane boyutları vardır, bu boyutları en ve boydur. İki boyutlu şekiller uzunluğun yanında birde alana sahiptirler. Dikdörtgenler prizması, kare prizma, küp ve benzeri şekiller üç boyutludur. Üç tane boyuta sahiptirler, bu boyutları en, boy ve yüksekliktir (kalınlık). Üç boyutlu şekillere madde yada cisim denir. Üç boyutlu şekillerde uzunluk ve alandan başka hacimde bulunur.
Birim Küplerden Hacim Ölçme Konu Anlatımı
Bir nesnenin yada maddenin uzayda (boşlukta) kapladığı yere hacim denir. Elle tutulabilen her maddenin bir hacmi vardır. Yalnız kare, dikdörtgen, üçgen gibi çokgenler ile doğru, doğru parçası, ışın ve benzeri geometrik şekillerin hacmi yoktur.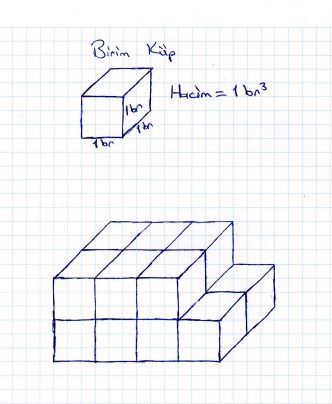 Bir kenar uzunluğu 1 birim olan küpün hacmi 1 birim küptür. Bundan yararlanarak birim küplerden oluşan bir yapının hacmini bulabiliriz. Yanda bulunan yapı 14 tane birim küpün yan yana ve üst üste gelmesinden oluşmuştur. Dolayısıyla bu yapının hacmi bir tane birim küpün hacminin 14 katına eşittir. Yani 14 tane birim küpten oluşmuş olan bu yapının hacmi 14 birim küptür.
Bir kenar uzunluğu 1 birim olan küpün hacmi 1 birim küptür. Bundan yararlanarak birim küplerden oluşan bir yapının hacmini bulabiliriz. Yanda bulunan yapı 14 tane birim küpün yan yana ve üst üste gelmesinden oluşmuştur. Dolayısıyla bu yapının hacmi bir tane birim küpün hacminin 14 katına eşittir. Yani 14 tane birim küpten oluşmuş olan bu yapının hacmi 14 birim küptür.
Yandaki yapıda 14 tane birim küp bulunduğunu sayarak bulabiliriz, fakat bazı durumlarda çok daha fazla birim küp olabilir, bu durumda sayması zor olacaktır, aynı dikdörtgenler prizması şeklindeki kutuda bulunan küp şekerlerin kaç adet olduğunu saymanın zor olduğu gibi. Bu durumda çarpma yaparak da kaç adet birim küp olduğunu bulabiliriz. Yukarıdaki şekilde yan yana 4 sıra, üst üste 2 sıra ve arka arkaya da 2 sıra vardır. Dolayısıyla bu sayıları çarparsak; 4.2.2=16 buluruz. Yalnız üste 2 tane boşluk bulunduğundan 16’dan 2 çıkarmalıyız. Yani 16-2=14 tane birim küp vardır. Bu yöntemi her zaman kullanabiliriz. Yöntemi tekrar hatırlayacak olursak; birim küplerden oluşan bir yapıda toplam kaç adet birim küp olduğunu bulmak için yan yana, arka arkaya ve üst üste kaç sıra olduğunu bulup çarpmamız yeterlidir, bu bize yapıdaki toplam birim küp sayısını verecektir.
Konu ile ilgili test çözmek için tıklayın.



