Sevgili öğrenciler pisagor bağıntısı konu anlatımı sayfamıza hoş geldiniz. Pisagor bağıntısı matematiğin en bilinen, en ünlü bağıntılarından biridir. Pisagor tarafından bulunmuş ve bu bağıntıya pisagor kendi ismini vermiştir. Bu bağıntıyı aslında ilk olarak pisagor’un bulmadığı da söylenir; fakat bunların hepsi ispata mahkumdur.[mathjax]
Bu bağıntı ile öğrencilik hayatımız boyunca sık sık karşılaşacağımızı söyleyebiliriz. LGS, TYT, KPSS gibi ismini duyup duymadığımız bir çok sınavda bu konudan soru çıkmaktadır. Konuyu dikkatlice incelemenizi tavsiye eder, hepinize başarılar dileriz.
Pisagor Bağıntısı Konu Anlatımı
» Bir dik üçgende 90 derecelik açının karşısında bulunan kenara Hipotenüs denir.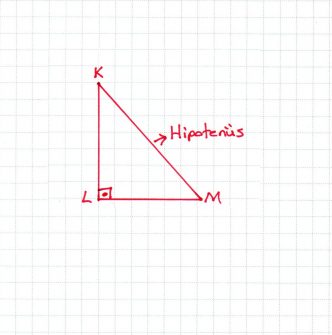 » Dik üçgenlerde her zaman en uzun kenar hipotenüstür.
» Dik üçgenlerde her zaman en uzun kenar hipotenüstür.
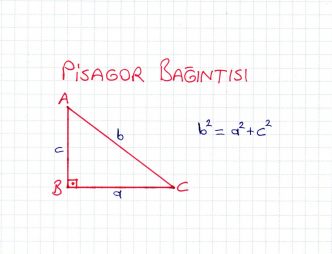 » Bir dik üçgende hipotenüsün uzunluğunun karesi, dik kenarların uzunluklarının kareleri toplamına eşittir. Bu bağıntıya Pisagor Bağıntısı denir.
» Bir dik üçgende hipotenüsün uzunluğunun karesi, dik kenarların uzunluklarının kareleri toplamına eşittir. Bu bağıntıya Pisagor Bağıntısı denir.
NOT: Pisagor Bağıntısını kullanabilmemiz için üçgenin dik üçgen olması gereklidir. Dik üçgenlerde herhangi 2 kenar uzunluğu verilirse pisagor bağıntısı yardımıyla 3.kenarın uzunluğunu bulabiliriz.
ÖRNEK: Aşağıdaki örnekte x’i bulalım.
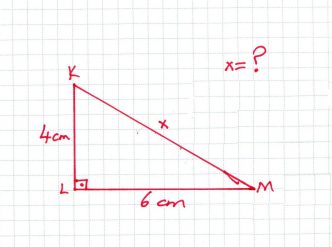 ÇÖZÜM: x, 90 derecenin karşısında olduğu için hipotenüstür.
ÇÖZÜM: x, 90 derecenin karşısında olduğu için hipotenüstür.
» Pisagor bağıntısını kurarsak;
x² = 4² + 6² = 16 + 36 = 52
$$\sqrt{x^2}=\sqrt{52}$$
$$x=2\sqrt{13}$$ cm olur.
ÖRNEK: Aşağıdaki örnekte x’i bulalım.
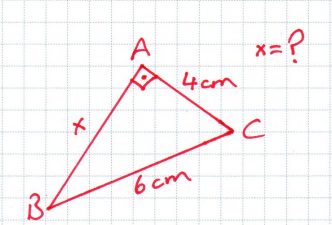 ÇÖZÜM: Bu örnekte hipotenüs uzunluğu verilmiştir, 6 cm lik uzunluk hipotenüstür.
ÇÖZÜM: Bu örnekte hipotenüs uzunluğu verilmiştir, 6 cm lik uzunluk hipotenüstür.
» Pisagor bağıntısını kurarsak;
6² = x² + 4²
36 = x² + 16
x² = 36-16
x² = 20
$$\sqrt{x^2}=\sqrt{20}$$
$$x=2\sqrt5$$ cm olur.
ÖRNEK: Aşağıdaki örnekte verilmeyen x uzunluğunu bulalım.
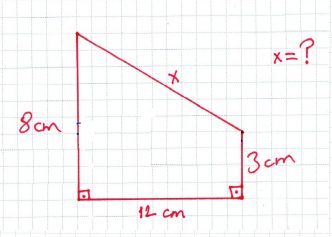 ÇÖZÜM: Bu tarz sorularda çizim yapmak gerekmektedir. Çizim yaparak x uzunluğu kenarlarından herhangi biri olan bir dik üçgen elde etmeliyiz.
ÇÖZÜM: Bu tarz sorularda çizim yapmak gerekmektedir. Çizim yaparak x uzunluğu kenarlarından herhangi biri olan bir dik üçgen elde etmeliyiz.
» Çizim yaptığımızda aşağıdaki gibi hipotenüs uzunluğu x, dik kenarları 5 ve 12 olan bir dik üçgen elde ederiz.
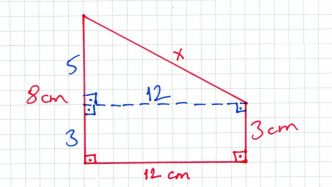 » Bu dik üçgende pisagor bağıntısını kurduğumuzda;
» Bu dik üçgende pisagor bağıntısını kurduğumuzda;
x² = 5² + 12² x² = 25 + 144
x² = 169
x = 13 cm bulunur.
Bazı Özel Dik Üçgenler
Kenar Uzunlukları Tam Sayı Olan Özel Dik Üçgenler
Aşağıda kenar uzunlukları verilen dik üçgenler pisagor bağıntısında en sık rastlanılan ve kenar uzunlukları tam sayı olan dik üçgenlerdir. Bu dik üçgenlerde en uzun kenarın hipotenüste olması gerektiği unutulmamalıdır. Kenar uzunlukları;
3-4-5 ve Katları
Bir dik üçgende dik kenarlardan biri 3’ün katı, diğeri 4’ün katı ise hipotenüs uzunluğu da 5’in aynı katı olacaktır. En sık karşılaşacağımız 3-4-5 üçgenleri şu uzunluklara sahiptir: 3-4-5 ; 6-8-10; 9-12-15 ; 12-16-20 ; 15-20-25 ; 30-40-50 vb.
5-12-13 ve Katları
Bir dik üçgende dik kenarlardan biri 5’in katı, diğeri 12’nin katı ise hipotenüs uzunluğu da 13’ün aynı katı olacaktır. En sık karşılaşacağımız 5-12-13 üçgenleri şu uzunluklara sahiptir: 5-12-13 ; 10-24-26 ; 15-36-39 vb.
8-15-17 ve Katları
Bir dik üçgende dik kenarlardan biri 8’in katı, diğeri 15’in katı ise hipotenüs uzunluğu da 17’nin aynı katı olacaktır. En sık karşılaşacağımız 8-15-17 üçgenleri şu uzunluklara sahiptir: 8-15-17 ; 16-30-34 ; 24-45-51 vb.
7-24-25 ve Katları
Bir dik üçgende dik kenarlardan biri 7’nin katı, diğeri 24’ün katı ise hipotenüs uzunluğu da 25’in aynı katı olacaktır. En sık karşılaşacağımız 7-24-25 üçgenleri şu uzunluklara sahiptir: 7-24-25 ; 14-48-50 ; 21-72-75 vb.
9-40-41 ve Katları
Bir dik üçgende dik kenarlardan biri 9’un katı, diğeri 40’ın katı ise hipotenüs uzunluğu da 41’in aynı katı olacaktır. En sık karşılaşacağımız 79-40-41 üçgenleri şu uzunluklara sahiptir: 9-40-41 ; 18-80-82 ; 27-120-123 vb.
NOT: Bir dik üçgende bu sayılardan herhangi ikisini gördüğünüzde diğerini pisagor bağıntısını yazmaya gerek duymadan hemen bulabilirsiniz. Sadece dik üçgenin en uzun kenarının hipotenüse karşılık geldiğinden emin olmalısınız. Yani eğer bir dik üçgende 3 cm ve 4 cm lik uzunluklar var ise verilmeyen uzunluk 5 cm’dir diyemeyiz. Eğer 5 cm hipotenüse denk geliyorsa bu doğru olur; aksi halde yanlıştır ve verilmeyen uzunluk pisagor bağıntısı yardımı ile hesaplanarak bulunmalıdır.
Diğer Bazı Özel Dik Üçgenler
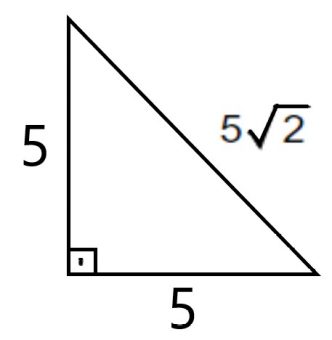
- En sık rastlanılan özel dik üçgenlerden biri ikiz kenar dik üçgendir. Bir ikiz kenar dik üçgende hipotenüs uzunluğu her zaman dik kenarlardan herhangi binin $$\sqrt2$$ katına eşittir. Aşağıdaki görselde bir ikiz kenar dik üçgenin kenarlarının uzunlukları verilmiştir.
- Karşımıza çıkması muhtemel özel dik üçgenlerden biri de şu şekildedir; eğer bir dik üçgende dik kenarlardan biri diğerinin 2 katı ise hipotenüs uzunluğu her zaman kısa olan dik kenarın $$\sqrt5$$ katına eşittir. Aşağıdaki görselde bu kurala uyan bir dik üçgen verilmiştir.
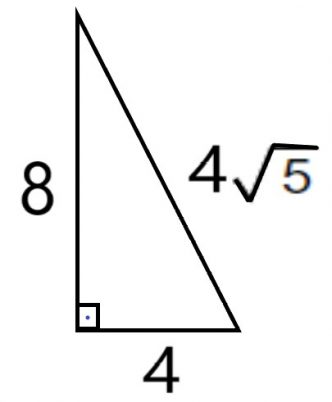
Konu ile ilgili test çözmek için tıklayınız.



