Bu konuda birinci dereceden bir bilinmeyenli eşitsizlikler kurmayı, verilen eşitsizliklere uygun cümleler söylemeyi, bu eşitsizlikleri çözüp çözüm kümelerini (eşitsizliği sağlayan sayıları) bulmayı ve eşitsizlikleri sayı doğrusu üzerinde göstermeyi öğreneceğiz. 8.Sınıf eşitsizlikler konu anlatımı ilk defa bu sınıfta işleyecek olduğumuz daha önce öğrenmediğimiz bir konudur, fakat liseye geçtiğimizde bu konuyla yine karşılaşacağız. Başarılar dileriz.[mathjax]
Eşitsizlikler Konu Anlatımı
İçerisinde $$<\;,\;>\;,\;\leq\;,\;\geq$$ sembolleri bulunan ifadelere eşitsizlik denir. Eşitsizliklerin söylenişleri şu şekildedir:
< → Küçüktür
> → Büyüktür
$$\leq$$ → Küçük eşittir (Küçüktür veya eşittir)
$$\geq$$ → Büyük eşittir (Büyüktür veya eşittir)
ÖRNEK: Aşağıdaki cümlelerin karşılarına uygun eşitsizlikleri yazalım.
5’ten büyük sayılar → x>5
Ali’nin yaşı 20’den küçüktür → a<20
18 ve 18 yaşından büyükler ehliyet alabilirler → e$$\geq$$18
Bir sayının 2 katının 3 eksiği 10’dan küçüktür → 2s-3<10
Bir sayının 7 fazlasının 3 katı 20’ye eşittir veya 20’den büyüktür → 3.(x+7)$$\geq$$20
Şehir içi hız limiti 50 km’dir → h$$\leq$$50
Bir sayının 5 eksiğinin 3 katı aynı sayının 6 katının 2 fazlasından küçüktür → 3.(x-5)<6x+2
Bir tartı en fazla 250 kilogramlık ağırlıkları tarta bilmektedir → $$a\leq250$$
-2’den büyük 7’den küçük sayılar → -2<x<7
Notu 45’ten düşük olanlar dersi geçemez → n<45
Not ortalaması 70 ve 70’ten büyük 85’ten küçük olanlar teşekkür alır → $$70\leq n<85$$
Not ortalaması 85 ve üzeri olanlar taktir belgesini hak eder → $$n\geq85$$
Bir sayının 3 fazlasının yarısı 25’ten büyüktür → $$\frac{x+3}2>25$$
Bir sayının 4 fazlasının 5’te 3’ü 40’tan fazladır → $$\frac{\displaystyle3(y+4)}5>40$$
ÖRNEK: Aşağıdaki eşitsizliklerin karşılarına uygun matematiksel cümleleri yazalım.
a<-5 → -5’ten küçük sayılar
$$k\geq1$$ → 1’e eşit ve 1’den büyük sayılar
5x+3>10 → 5 katının 3 fazlası 10’dan büyük olan sayılar
$$2(x-10)\leq80$$ → 10 eksiğinin 2 katı 80’e eşit ve 80’den küçük olan sayılar
$$\frac a2>15$$ → Yarısı 15’ten büyük olan sayılar
Eşitsizliklerin Sayı Doğrusunda Gösterimi
Eşitsizlikler sayı doğrusu üzerinde gösterilirken eşitsizlik sembolüne dikkat etmemiz gerekmektedir. < ve > sembollerinde sayılar çözüm kümesine dahil değilken, $$\leq$$ ve $$\geq$$ sembollerinde sayılar çözüm kümesine dahildir. Yani;
x<3 eşitsizliğine göre bu eşitsizliği sağlayan sayılar 3’ten küçük olan bütün reel sayılardır, 3 ise bu eşitsizliği sağlamamaktadır.
x$$\leq$$3 eşitsizliğine göre ise bu eşitsizliği sağlayan sayılar 3 ve 3 ten küçük olan bütün reel sayılardır.
ÖRNEK: Aşağıda bazı eşitsizlikler ve bu eşitsizliklerin sayı doğrusu üzerinde gösterimleri verilmiştir. Dikkatle inceleyiniz.
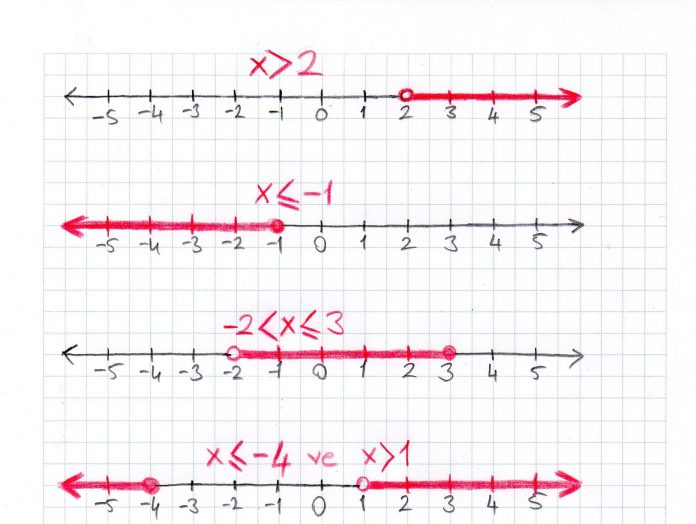
Yukarıdaki resimde eşitsizlikler ve eşitsizliklerin sayı doğrusu üzerindeki karşılıkları çizilmiştir. Eşitsizliklerin sayı doğrusu üzerindeki karşılıkları kırmızı renkle çizilen kısımlardır. Kırmızı renkle çizilen kısımlarda yer alan bütün reel sayılar o eşitsizliği sağlayan sayılardır.
Eşitsizlikler sayı doğrusunda gösterilirken küçüktür ve büyüktür sembollerinde sayının karşısına daire çizilir, dairenin içi boş bırakılır. Küçük eşittir ve büyük eşittir de ise sayıların karşısına çizilen dairelerin içleri doldurulur. Dolu daire o sayının çözüm kümesinde yer aldığını gösterirken, boş daire o sayının çözüm kümesinde olmadığı anlamını taşır.
Eşitsizliklerin Çözümü
Sevgili öğrenciler, eşitsizliklerin çözümü aynı denklem çözümü gibidir. Denklemi çözdüğümüz mantık ile eşitsizlikleri çözeriz. Amacımız bilinmeyeni eşitsizliğin herhangi bir tarafında yalnız başına bırakmaktır. Bunun için bilinmeyenin yanındaki sayılardan sırası ile kurtuluruz. Bu sıra işlem önceliği sırasının tersten işletilmesidir. Eşitsizlikleri çözerken aşağıdaki maddelere dikkat etmemiz gerekmektedir:
- Eşitsizliklerin her iki tarafına aynı sayı eklenir veya her iki tarafından aynı sayı çıkarılırsa eşitsizlik yön değiştirmez.
- Bir eşitsizliğin her iki tarafı aynı pozitif sayı ile çarpılır veya aynı pozitif sayıya bölünürse eşitsizlik yön değiştirmez.
- Bir eşitsizliğin her iki tarafı aynı negatif sayı ile çarpılır veya aynı negatif sayıya bölünürse eşitsizlik yön değiştirir.
NOT: Eşitsizlik sadece negatif sayılar ile çarpma veya bölme yaptığımızda yön değiştirir, onun haricinde yön değiştirmez.
ÖRNEK: $$2x+7\leq23$$ eşitsizliğinin çözüm kümesini bulalım.
ÇÖZÜM: $$2x+7\leq23$$ eşitsizliğinin çözüm kümesini bulurken sırası ile aşağıdaki adımlar izlenir:
1) ilk olarak 7 sayısından kurtulmamız gerekir, bunun için eşitsizliğin her iki tarafından 7 çıkartırız.
$$2x+7{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}7}\leq23{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}7}$$
$$2x\leq16$$ elde ederiz.
2) Eşitsizliğin her iki tarafı 2’ye böleriz.
$$\frac{2x}{\color[rgb]{1.0, 0.0, 0.0}2}\leq\frac{16}{\color[rgb]{1.0, 0.0, 0.0}2}$$
$$x\leq8$$ elde ederiz ve bu eşitsizliğimizin çözüm kümesi olur.
ÖRNEK: $$5<-3y+8\leq14$$ eşitsizliğini çözelim.
ÇÖZÜM: $$5<-3y+8\leq14$$ eşitsizliğini çözerken sırası ile aşağıdaki adımları izlememiz gerekir.
1) Önce eşitsizliğin her tarafından 8 çıkarırız.
$$5{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}8}<-3y+8{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}8}\leq14{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}8}$$
$$-3<-3y\leq6$$ bulunur.
2) Eşitsizliğin her tarafını -3’e bölmeliyiz. Yalnız negatif bir sayıya böldüğümüz için eşitsizliklerin yönünü değiştirmeyi unutmamalıyız.
$$\frac{-3}{{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}3}}{\color[rgb]{1.0, 0.0, 0.0}>}\frac{-3y}{{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}3}}{\color[rgb]{1.0, 0.0, 0.0}\geq}\frac6{{\color[rgb]{1.0, 0.0, 0.0}-}{\color[rgb]{1.0, 0.0, 0.0}3}}$$
Bu işlemin sonucunda $$1>y\geq-2$$ bulunur. Bu eşitsizliği sayılar küçükten büyüğe doğru olacak şekilde düzenlersek;
$$-2\leq y<1$$ olur.
Konu ile ilgili test çözmek için tıklayınız.



